Sum All Prime Numbers Challenge in JavaScript

Introduction

Sum All Primes is a coding challenge in which we have to find the sum of all prime numbers up to a given number. We’ll be given a number, such as 10, and first need to find all the prime numbers up to that number. Then, to get the final output, we need to sum all the prime numbers that we found in the first step.

To solve this problem, we will need to take two major steps. Although this can be solved in any programming language, we’ll use JavaScript.

Example

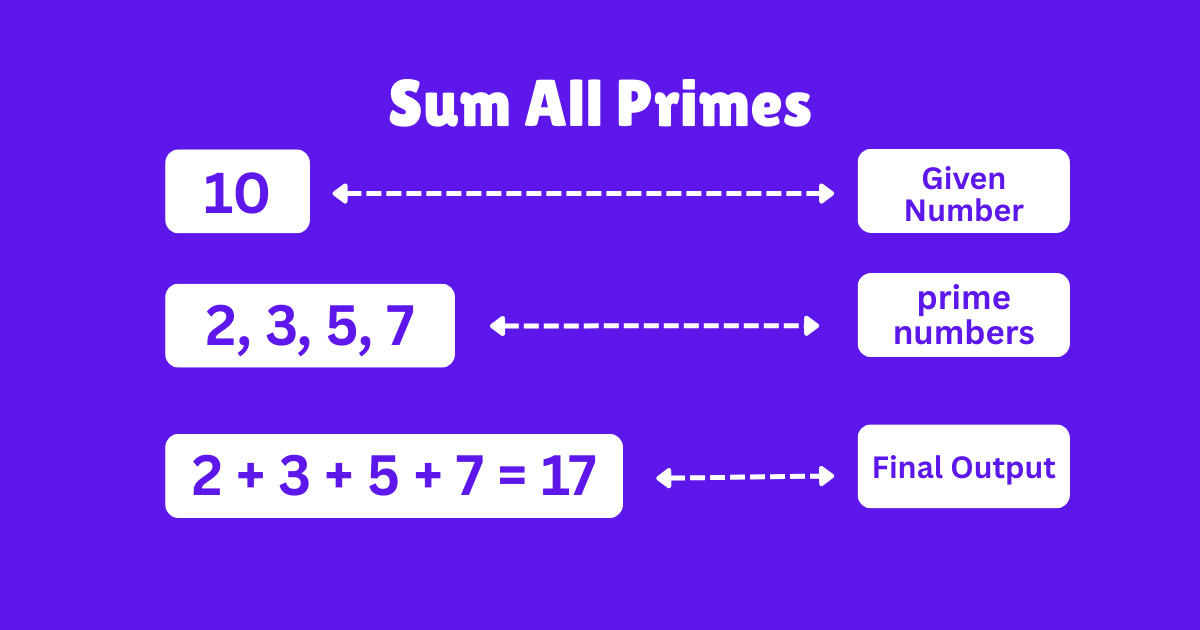
let num = 10;

Step 1: We need to find all the prime numbers up to the given number, which is num (10).

A prime number is a whole number greater than 1 that is only divisible by 1 and itself. For example, 2 is only divisible by 1 and 2.

The prime numbers up to 10 are:

2, 3, 5, 7

These are the prime numbers in the range of 10. As you can see, each of these numbers is only divisible by 1 and by itself.

Step 2: In the second and final step, we need to sum all these prime numbers (2, 3, 5, 7) to get the final output.

2 + 3 + 5 + 7 = 17

So, 17 is the final output.

Solution

function sumPrimes(num) {


  function isPrime(num) {
    // Handle edge cases
    if (num <= 1) return false; // Numbers less than or equal to 1 are not prime
    if (num === 2) return true; // 2 is a prime number
    if (num % 2 === 0) return false; // All even numbers greater than 2 are not prime


    // Check divisibility from 3 to sqrt(num)
    for (let i = 3; i <= Math.sqrt(num); i += 2) {
      if (num % i === 0) {
        return false; // If divisible, it's not a prime number
      }
    }


    return true; // If no divisors found, it's a prime number
  }
  let sumPrime = 0;


  for (let i = 0; i <= num; i++) {
    if (isPrime(i)) {
      sumPrime += i;
    }
  }
  return sumPrime;


}


sumPrimes(10);

Let’s simplify it further by breaking this down for better understanding:

As you can see, we have a function called sumPrimes with one parameter, num, where the number value will be stored. Now we need to write the logic within this function to solve the problem.

As we already know, this challenge has two major parts to solve, which we’ve already mentioned above. In the first step, we need to identify all the prime numbers within the range of numbers we are given. In the second step, we need to find the sum of all the prime numbers identified in the first step.

For the first step, we wrote another function, isPrime, within the sumPrimes function, which will help us find only the prime numbers within the range of the given number. Here’s how it works

function isPrime(num) {
   // Handle edge cases
   if (num <= 1) return false;  // Numbers less than or equal to 1 are not prime
   if (num === 2) return true;  // 2 is a prime number
   if (num % 2 === 0) return false; // All even numbers greater than 2 are not prime


   // Check divisibility from 3 to sqrt(num)
   for (let i = 3; i <= Math.sqrt(num); i += 2) {
       if (num % i === 0) {
           return false; // If divisible, it's not a prime number
       }
   }


   return true; // If no divisors found, it's a prime number 
}

We passed the same num as a parameter into isPrime function, which means it will work on the same number that was provided to us for solving this challenge.

As you can see below, within the isPrime function, we wrote the first step to include some conditions that will return true or false based on the provided number.

if (num <= 1) return false;  
if (num === 2) return true;
if (num % 2 === 0) return false;

If all of these conditions are true, it will proceed with the number. As we know, a prime number is a number greater than one that is divisible only by 1 and itself. So, in our first condition, if the given number is 1, it will return false, meaning there is no prime number in this range. If the given number is 2, it will return true, indicating that it is a prime number. In the third condition, if the given number is divisible by 2, it will return false, meaning the number is not prime.

In the next step, you wrote this block of code, which you can see below:

for (let i = 3; i <= Math.sqrt(num); i += 2) {
 if (num % i === 0) {
   return false; // If divisible, it's not a prime number
 }
}

i = 3: Starts checking from 3, skipping even numbers (since even numbers greater than 2 are not prime).

i <= Math.sqrt(num): Loops up to the square root of num, which reduces the number of checks needed.

i += 2: Increments i by 2, so it checks only odd numbers, because even numbers greater than 2 can't be prime.

if (num % i === 0): If num is divisible by any odd numbers between 3 and sqrt(num), it returns false, indicating that the number is not prime.

Finally, we will return true, which means the number is prime, as we did at the end of the isPrime function.

As we know, we now have a function called isPrime that helps us filter out all the prime numbers up to the range of the provided number.

In our second step, we need to find the sum of all the prime numbers, as you can see below:

let sumPrime = 0;
 for(let i = 0; i <= num; i++) {
   if(isPrime(i)) {
     sumPrime += i;
   }
}

We first declared a variable, sumPrime, and assigned 0 as its initial value, which we will update later to hold the final sum of all prime numbers.

Next, we started a for loop, beginning from zero, as usual, and running up to the number num. Within the loop, we wrote an if condition to verify whether the number passed as an argument to the function is prime. If the number is prime, it will be added to the sumPrime variable that we declared earlier.

Finally, we return the sumPrime variable as the final output.